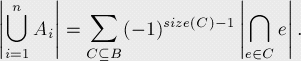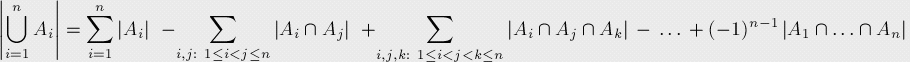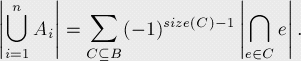黑马程序员技术交流社区
标题: 容斥原理，解决多重复问题最好的办法 [打印本页]
作者: 永远的EOF 时间: 2015-8-19 23:20
标题: 容斥原理，解决多重复问题最好的办法
容斥原理是一种重要的组合数学方法，可以让你求解任意大小的集合，或者计算复合事件的概率。
描述 容斥原理可以描述如下：
要计算几个集合并集的大小，我们要先将所有单个集合的大小计算出来，然后减去所有两个集合相交的部分，再加回所有三个集合相交的部分，再减去所有四个集合相交的部分，依此类推，一直计算到所有集合相交的部分。
关于集合的原理公式 上述描述的公式形式可以表示如下：
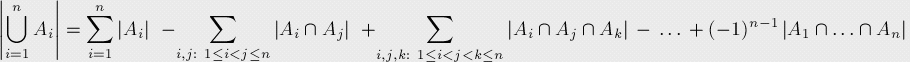
它可以写得更简洁一些，我们将B作为所有Ai的集合，那么容斥原理就变成了：
这个公式是由 De Moivre (Abraham de Moivre)提出的。
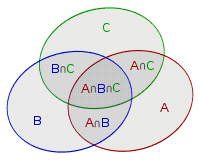
关于维恩图的原理 用维恩图来表示集合A、B和C：
那么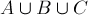
的面积就是集合A、B、C各自面积之和减去
, 
, 
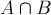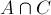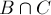的面积，再加上
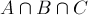的面积。 由此，我们也可以解决n个集合求并的问题。
关于概率论的原理 设事件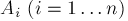
，
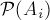代表发生某些事件的概率（即发生其中至少一个事件的概率），则： 这个公式也可以用B代表Ai的集合：
容斥原理的证明 我们要证明下面的等式：
其中B代表全部Ai的集合
我们需要证明在Ai集合中的任意元素，都由右边的算式被正好加上了一次（注意如果是不在Ai集合中的元素，是不会出现在右边的算式中的）。
假设有一任意元素在k个Ai集合中（k>=1），我们来验证这个元素正好被加了一次：
当size(C)=1时，元素x被加了k次。
当size(C)=2时，元素x被减了C(2,k)次，因为在k个集合中选择2个，其中都包含x。
当size(C)=3时，元素x被加了C(3,k)次。
……
当size(C)=k时，元素x被加/减了C(k,k)次，符号由sign(-1)^(k-1)决定。
当size(C)>k时，元素x不被考虑。
然后我们来计算所有组合数的和。
由二项式定理，我们可以将它变成：
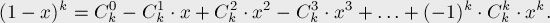
我们把x取为1，这时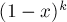
表示1-T（其中T为x被加的总次数），所以
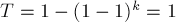，证明完毕。
作者: sven556677 时间: 2015-8-20 08:34
问题是：跟我学java的关系在哪？
| 欢迎光临 黑马程序员技术交流社区 (http://bbs.itheima.com/) |
黑马程序员IT技术论坛 X3.2 |
