有一句话说得好,要有造轮子的技术和用轮子的觉悟,今年来人工智能火的不行,大家都争相学习机器学习,作为学习大军中的一员,我觉得最好的学习方法就是用python把机器学习算法实现一遍,下面我介绍一下用逻辑回归实现手写字体的识别。
逻辑回归知识点回顾 线性回归简单又易用<span class="MathJax" id="MathJax-Element-18-Frame" tabindex="0" data-mathml="hθ(x)=θTx" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">hθ(x)=θTxhθ(x)=θTx,可以进行值的预测,但是不擅长分类。在此基础上进行延伸,把预测的结果和概率结合起来就可以做分类器了,比如预测值大于0.5,则归为1类,否则就归为0类,这个就是逻辑回归算法了。逻辑回归主要解决的就是二分类问题,比如判断图片上是否一只猫,邮件是否垃圾邮件等。
由于逻辑回归的结果是概率值,为0-1之间,因此需要在线性回归的结果上增加一次运算,使得最后的预测结果在0到1之间。
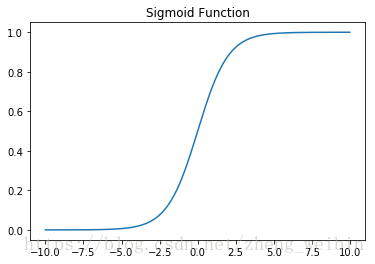
Sigmoid函数,表达式为:<span class="MathJax" id="MathJax-Element-19-Frame" tabindex="0" data-mathml="g(z)=11+e−z" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">g(z)=11+e−zg(z)=11+e−z
sigmoid的输出在0和1之间,我们在二分类任务中,采用sigmoid的输出的是事件概率,也就是当输出满足满足某一概率条件我们将其划分正类。
结合了sigmoid函数,把线性回归的结果概率化,得到预测函数为<span class="MathJax" id="MathJax-Element-20-Frame" tabindex="0" data-mathml="hθ(x(i))=g(θTx(i))" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">hθ(x(i))=g(θTx(i))hθ(x(i))=g(θTx(i)),<span class="MathJax" id="MathJax-Element-21-Frame" tabindex="0" data-mathml="g(z)=11+e−z" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">g(z)=11+e−zg(z)=11+e−z。当概率大于0.5时为1类,否则判定位0类。
接下来我们开始使用逻辑回归进行手写字体的识别!
此次使用的是5000条手写数字的数据。一条训练数据是20px*20px图片的数据,每一个像素点是代表灰度值。我们查看一下前100条手写数据,如下图:
数据集下载地址:
定义向量化的预测函数hθ(x)hθ(x)首先我们定义预测函数<span class="MathJax" id="MathJax-Element-23-Frame" tabindex="0" data-mathml="hθ(x(i))=g(θ0+θ1x1(i)+θ2x2(i)+...+θkxk(i))" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">hθ(x(i))=g(θ0+θ1x(i)1+θ2x(i)2+...+θkx(i)k)hθ(x(i))=g(θ0+θ1x1(i)+θ2x2(i)+...+θkxk(i)) ,k是参数的个数。
写成向量化的形式为:
<span class="MathJax" id="MathJax-Element-24-Frame" tabindex="0" data-mathml="hθ(x(i))=g(θTx(i))" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">hθ(x(i))=g(θTx(i))hθ(x(i))=g(θTx(i)) , <span class="MathJax" id="MathJax-Element-25-Frame" tabindex="0" data-mathml="g(z)=11+e−z" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">g(z)=11+e−zg(z)=11+e−z ,g(z)是激活函数(sigmoid function)
def h(mytheta,myX):#expit是scipy库中向量化sigmoid函数的计算函数 return expit(np.dot(myX, mytheta))预测函数中<span class="MathJax" id="MathJax-Element-26-Frame" tabindex="0" data-mathml="θ" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">θθ的值是未知的,接下来的任务就是要根据训练集,求解出<span class="MathJax" id="MathJax-Element-27-Frame" tabindex="0" data-mathml="θ" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">θθ的值。
计算代价函数(Cost Function)在线性回归中的最小二乘法,求解参数<span class="MathJax" id="MathJax-Element-28-Frame" tabindex="0" data-mathml="θ" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">θθ就是最小化残差平方和,也就是代价函数<span class="MathJax" id="MathJax-Element-29-Frame" tabindex="0" data-mathml="J(θ)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">J(θ)J(θ)。代价函数<span class="MathJax" id="MathJax-Element-30-Frame" tabindex="0" data-mathml="J(θ)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">J(θ)J(θ)是度量预测错误的程度,逻辑回归的代价函数为对数似然函数,
等价于:
<span class="MathJax" id="MathJax-Element-31-Frame" tabindex="0" data-mathml="J(θ)=1m∑i=1m[−y(i)log(hθ(x(i)))−(1−y(i))log(1−hθ(x(i)))]" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">J(θ)=1m∑mi=1[−y(i)log(hθ(x(i)))−(1−y(i))log(1−hθ(x(i)))]J(θ)=1m∑i=1m[−y(i)log(hθ(x(i)))−(1−y(i))log(1−hθ(x(i)))]
def computeCost(mytheta,myX,myy): m = len(X) #5000 term1 = np.dot(-np.array(myy).T,np.log(h(mytheta,myX)))#shape(1,401) term2 = np.dot((1-np.array(myy)).T,np.log(1-h(mytheta,myX)))#shape(1,401) return float((1./m) * np.sum(term1 - term2) )使得预测错误的程度最低,即使得<span class="MathJax" id="MathJax-Element-32-Frame" tabindex="0" data-mathml="J(θ)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">J(θ)J(θ)最小,此时我们把问题转为最优化问题。
下面介绍一种求解最优化的算法:梯度下降。从初始位置每次向梯度方向(就是下降速度最快的方向)迈一小步,一直走到最低点。想象你在下山,你朝着当前位置下降最快的方向走一步。
经过数学运算可以得出<span class="MathJax" id="MathJax-Element-33-Frame" tabindex="0" data-mathml="∂J∂θ=1m∑i=1m(hθ(x(i))−y(i)xj(i))" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">∂J∂θ=1m∑mi=1(hθ(x(i))−y(i)x(i)j)∂J∂θ=1m∑i=1m(hθ(x(i))−y(i)xj(i))。
def costGradient(mytheta,myX,myy): m = myX.shape[0] beta = h(mytheta,myX)-myy.T #shape: (5000,1) grad = (1./m)*np.dot(myX.T,beta) #shape: (401, 5000) return grad #shape: (401, 1)这里我们使用的是高级算法,scipy中的optimize,求解最小化<span class="MathJax" id="MathJax-Element-36-Frame" tabindex="0" data-mathml="J(θ)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">J(θ)J(θ)时<span class="MathJax" id="MathJax-Element-37-Frame" tabindex="0" data-mathml="θ" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">θθ的值。
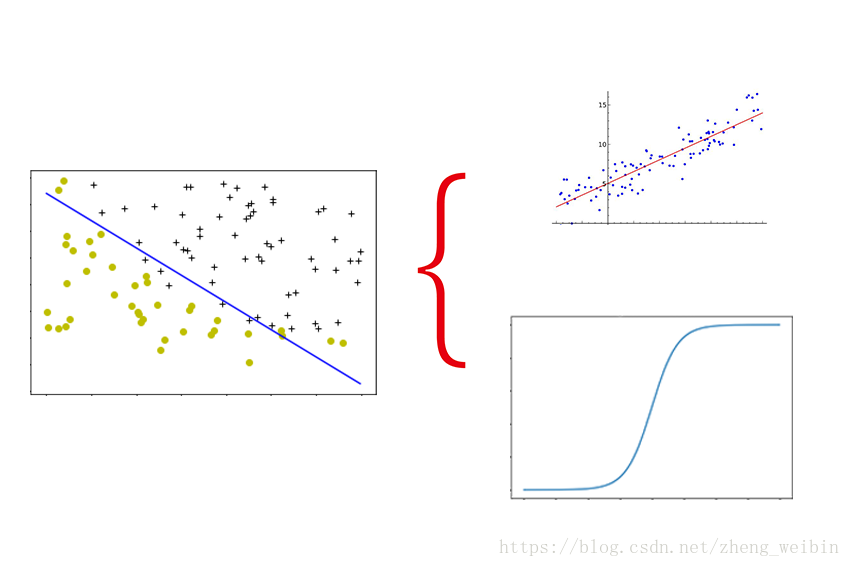
from scipy import optimizedef optimizeTheta(mytheta,myX,myy): result = optimize.fmin_cg(computeCost, fprime=costGradient, x0=mytheta, \ args=(myX, myy), maxiter=50, disp=False,\ full_output=True) return result[0], result[1]逻辑回归擅长二分类问题,因此需要把多分类问题转换为多个二分类问题进行解决。如下图,首先把蓝色和绿色标记看为一类,红色记为一类,这样子就可以用预测函数<span class="MathJax" id="MathJax-Element-38-Frame" tabindex="0" data-mathml="hθ(x)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">hθ(x)hθ(x)计算出新数据为红色类别的概率,同理也可以计算出新数据为蓝色、绿色类别的概率,选择概率最高的类别作为新数据的预测分类,这就是One-VS-All多分类算法。
计算测试集得到逻辑回归预测的准确度为 89.1%。抽看第1601个数据观察预测情况
predictOneVsAll(Theta,X[1600])#3scipy.misc.toimage(X[1600][1:].reshape(20,20).T)画出第1601个数据
逻辑回归的预测准确率是89.1%,那么以逻辑回归作为神经元的神经网络算法,是否会更加强大呢,我们下期见!

| 欢迎光临 黑马程序员技术交流社区 (http://bbs.itheima.com/) | 黑马程序员IT技术论坛 X3.2 |