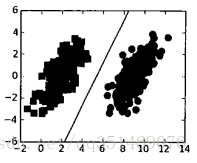
如上图, 他们之间已经分隔的足够开, 可以很容易在图中做一条直线将两组数据分开, 这种情况下, 这组数据被称为”线性可分数据”

这组数据, 就是”线性不可分数据”
SVM是最好的现成分类器, 这里的“现成”指的是分类器不加修改即可直接使用。同时,这就意味着在数据集上采用原始的数据就可以用SVM得到低错误率的结果, SVM也能够对数据集之外的数据点做出很好的分类决策
本文章只关注最流行的一种实现, 叫 “序列最小优化算法(一种求解支持向量机二次规划的算法)”,在此之后,将介绍“核函数”, 它的作用的将SVM扩展到更多的数据集上
优点:
缺点:
适用数据类型:

如上图, 他们之间已经分隔的足够开, 可以很容易在图中做一条直线将两组数据分开, 这种情况下, 这组数据被称为”线性可分数据”

这组数据, 就是”线性不可分数据”
上述将数据集分隔开来的直线称为分隔超平面
一维在坐标轴是个点, 二维在坐标轴是直线, 由于数据点都在二维上, 所以分隔超平面就是一条直线, 但是如果所给的数据集是三维, 那么用来分隔数据的就是一个平面, 三维以上形容不出来, 超出人类想象, 1024维需要1023维的某某对象来对数据进行分隔, 分隔的规律就是N-1维, 叫做“超平面”, 也就是决策边界, 分布在两边的数据属于两边的类别
数据点离决策边界越远,最后预测结果越可信
我们要找到离分隔超平面最近的点, 确保他们离分隔面的距离尽可能远, 这里点到分隔面的距离被称为间隔
这里有两个概念
我们希望间隔尽可能大, 这是因为如果我们犯错或在有限的数据上训练分类器的话,我们希望分类器尽可能不出现错误
支持向量就是 分隔…..离…..超平面…..最近的……那些点。接下来要最大化支持向量到分隔面的距离


| 欢迎光临 黑马程序员技术交流社区 (http://bbs.itheima.com/) | 黑马程序员IT技术论坛 X3.2 |