黑马程序员技术交流社区

标题: 【上海校区】区块链中的密码学技术——哈希算法、Merkle... [打印本页]

作者: 不二晨 时间: 2018-9-3 09:49
标题: 【上海校区】区块链中的密码学技术——哈希算法、Merkle...
【转载】 https://blog.csdn.net/s_lisheng/article/details/77937202

本文是学习区块链技术中关于密码学这一部分的相关知识点学习总结整理。

哈希算法哈希函数（散列函数）定义

公式表示形式：

h=H(m)h=H(m)

函数说明：
mm：任意长度消息（不同算法实现，长度限制不同，有的哈希函数（SHA-3）不限制消息长度，有的限制（SHA-2），但即使有限制其长度也非常大，可以认为是任意长度消息）
HH：哈希函数
hh：固定长度的哈希值

典型的散列函数都有非常大的定义域，比如SHA-2最高接受(<span class="MathJax" id="MathJax-Element-5-Frame" tabindex="0" data-mathml="264−1)/8" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; font-style: normal; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">264−1)/8264−1)/8长度的字节字符串。同時散列函數一定有着有限的值域，比如固定长度的比特串（例如：256,512）。在某些情况下，散列函数可以设计成具有相同大小的定义域和值域间的單射。

相关概念

哈希函数定义——密码哈希函数是一类数学函数，可以在有限合理的时间内，将任意长度的消息压缩为固定长度的二进制串，其输出值称为哈希值，也称散列值。
碰撞定义——是指两个不同的消息在同一哈希函数作用下，具有相同的哈希值。
哈希函数的安全性——是指在现有的计算资源（包括时间、空间、资金等）下，找到一个碰撞是不可行的。
抗弱碰撞性——对于给定的消息M1M1，要发现另一个消息M2M2，满足H(M1)=H(M2)H(M1)=H(M2)在计算上是不可行的。
抗强碰撞性——找任意一对不同的消息M1M1，M2M2，使H(M1)=H(M2)H(M1)=H(M2)在计算上是不可行的。
雪崩效应——当一个输入位发生变化时，输出位将有一半会发生变化。

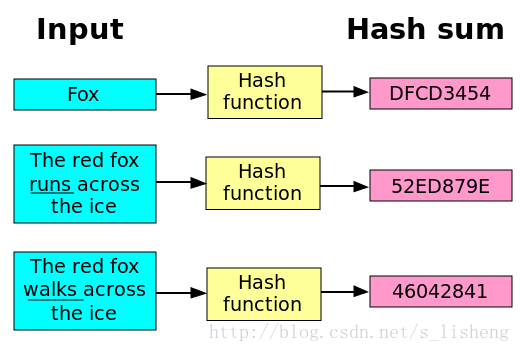
下图形象的说明了哈希函数：

哈希算法就是以哈希函数为基础构造的，常用于实现数据完整性和实体认证。一个优秀的 hash 算法，将能实现：

正向快速：给定明文和 hash 算法，在有限时间和有限资源内能计算出 hash 值。
逆向困难：给定（若干） hash 值，在有限时间内很难（基本不可能）逆推出明文。
输入敏感：原始输入信息修改一点信息，产生的 hash 值看起来应该都有很大不同。
冲突避免：很难找到两段内容不同的明文，使得它们的 hash 值一致（发生冲突）。

哈希函数的性质

抗碰撞性

哈希函数的抗碰撞性是指寻找两个能够产生碰撞的消息在计算上是不可行的。但找到两个碰撞的消息在计算上不可行，并不意味着不存在两个碰撞的消息。哈希函数是把大空间上的消息压缩到小空间上，碰撞肯定存在。只是计算上是不可行的。例如，如果哈希值的长度固定为256位，显然如果顺序取<span class="MathJax" id="MathJax-Element-12-Frame" tabindex="0" data-mathml="1,2,⋯,2256+1" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">1,2,⋯,2256+11,2,⋯,2256+1这<span class="MathJax" id="MathJax-Element-13-Frame" tabindex="0" data-mathml="2256+1" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">2256+12256+1个输入值，计算它们的哈希值，肯定能够找到两个输入值，使得它们的哈希值相同。

原像不可逆

原像不可逆，指的是知道输入值，很容易通过哈希函数计算出哈希值；但知道哈希值，没有办法计算出原来的输入值。

难题友好性

难题友好性指的是没有便捷的方法去产生一满足特殊要求的哈希值。

一个哈希函数<span class="MathJax" id="MathJax-Element-14-Frame" tabindex="0" data-mathml="H" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">HH称为难题友好的，如果对于每个<span class="MathJax" id="MathJax-Element-15-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn位的输出<span class="MathJax" id="MathJax-Element-16-Frame" tabindex="0" data-mathml="y" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">yy，若<span class="MathJax" id="MathJax-Element-17-Frame" tabindex="0" data-mathml="k" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">kk是从一个具有较高不可预测性（高小熵）分布中选取的，不可能以小于<span class="MathJax" id="MathJax-Element-18-Frame" tabindex="0" data-mathml="2n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">2n2n的时间找到一个<span class="MathJax" id="MathJax-Element-19-Frame" tabindex="0" data-mathml="x" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">xx，使<span class="MathJax" id="MathJax-Element-20-Frame" tabindex="0" data-mathml="H(k||x)=y" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">H(k||x)=yH(k||x)=y。

为了引申出工作量证明POW的原理，考虑一个由哈希函数构成的解谜问题：已知哈希函数<span class="MathJax" id="MathJax-Element-21-Frame" tabindex="0" data-mathml="H" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">HH，一个高小熵分布的值<span class="MathJax" id="MathJax-Element-22-Frame" tabindex="0" data-mathml="value" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">valuevalue以及目标范围<span class="MathJax" id="MathJax-Element-23-Frame" tabindex="0" data-mathml="Y" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">YY，寻找<span class="MathJax" id="MathJax-Element-24-Frame" tabindex="0" data-mathml="x" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">xx，使得<span class="MathJax" id="MathJax-Element-25-Frame" tabindex="0" data-mathml="H(value||x)∈Y" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">H(value||x)∈YH(value||x)∈Y。

这个问题等价于需要找到一个输入值，使得输出值落在目标范围<span class="MathJax" id="MathJax-Element-26-Frame" tabindex="0" data-mathml="Y" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">YY内，而<span class="MathJax" id="MathJax-Element-27-Frame" tabindex="0" data-mathml="Y" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">YY往往是所有的输出值的一个子集。实际上，如果一个哈希函数<span class="MathJax" id="MathJax-Element-28-Frame" tabindex="0" data-mathml="H" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">HH的输出位<span class="MathJax" id="MathJax-Element-29-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn位，那么输出值可以是任何一个<span class="MathJax" id="MathJax-Element-30-Frame" tabindex="0" data-mathml="0" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">00~<span class="MathJax" id="MathJax-Element-31-Frame" tabindex="0" data-mathml="2n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">2n2n范围内的值。预定义的目标范围<span class="MathJax" id="MathJax-Element-32-Frame" tabindex="0" data-mathml="Y" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">YY的大小决定了这个问题的求解难度。如果<span class="MathJax" id="MathJax-Element-33-Frame" tabindex="0" data-mathml="Y" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">YY包含所有<span class="MathJax" id="MathJax-Element-34-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn比特的串，那么问题就简单了，但如果<span class="MathJax" id="MathJax-Element-35-Frame" tabindex="0" data-mathml="Y" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">YY只包含一个元素，那么这个求解是最难的，相当于给定一个哈希值，找出其中一个原像，原像不可逆的性质说明了这个难度。事实上，由于<span class="MathJax" id="MathJax-Element-36-Frame" tabindex="0" data-mathml="value" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">valuevalue具有高小熵分布，这确保了除了随机尝试<span class="MathJax" id="MathJax-Element-37-Frame" tabindex="0" data-mathml="x" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">xx值以完成搜寻那个很大的空间外，没有其他有效的途径了。

哈希函数的难题友好性构成了基于工作量证明的共识算法的基础。通过哈希运算得出的符合特定要求的哈希值，可以作为共识算法中的工作量证明。这里比特币的安全保证依赖于哈希函数的安全性，如果哈希函数被攻破，可以想象POW共识算法就失效了，不用算力达到<span class="MathJax" id="MathJax-Element-38-Frame" tabindex="0" data-mathml="51%" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">51%51%就可以攻击了。

小熵（min-entropy）是信息理论中衡量某个结果的可预测性的一个指标。高小熵值的是变量呈均匀分布（随机分布）。如果我们从对分布的值进行随机抽样，不会经常抽到一个固定的值。例如，如果在一个128位的数中随机选一个固定的数<span class="MathJax" id="MathJax-Element-39-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn，那么选到该数的几率是<span class="MathJax" id="MathJax-Element-40-Frame" tabindex="0" data-mathml="1/2128" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">1/21281/2128。

典型哈希函数SHA256

SHA256属于SHA（Secure Hash Algorithm，安全哈希算法）家族一员，是SHA-2算法簇中的一类，对于小于<span class="MathJax" id="MathJax-Element-41-Frame" tabindex="0" data-mathml="264" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">264264位的消息，产生一个256位的消息摘要。

SHA-256其计算过程分为两个阶段：消息的预处理和主循环。在消息的预处理阶段，主要完成消息的填充和扩展填充，将所有输入的原始消息转换为<span class="MathJax" id="MathJax-Element-42-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn个512比特的消息块，之后对每个消息块利用SHA256压缩函数进行处理。下面讲述的是如何计算Hash值，目前还没有完全理解，列在这里是为了有个宏观的概念，大致知道是什么回事，以后需要的时候再深入学习理解。

SHA256计算步骤：

step1：附加填充比特。对报文进行填充使报文长度 <span class="MathJax" id="MathJax-Element-43-Frame" tabindex="0" data-mathml="n≡(448 mod 512)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">n≡(448 mod 512)n≡(448 mod 512)，填充比特数范围是1到512，填充比特串的最高位为1，其余位为0。（448=512-64，为了下面的64位）

step2 ：附加长度值。将用64-bit表示初始报文（填充前）的位长度附加在step1的结果后（低字节位优先）。

step3：初始化缓存。使用一个256bit的缓存来存放该哈希函数的中间值及最终结果。
缓存表示为：A=0x6A09E667 , B=0xBB67AE85 , C=0x3C6EF372 , D=0xA54FF53A,
E=0x510E527F , F=0x9B05688C , G=0x1F83D9AB , H=0x5BE0CD19

step4：处理512bit（16个字）报文分组序列。该算法使用了六种基本逻辑函数，由64步迭代运算组成。每步都以256-bit缓存值ABCDEFGH为输入，然后更新缓存内容。每步使用一个32-bit 常数值Kt 和一个32-bit Wt。Kt是常数值，在伪代码中有它的常数值定义。Wt是分组之后的报文，512 bit=32bit*16，也就是Wt t=1,2..16由该组报文产生。Wt t=17,18,..,64由前面的Wt按递推公式计算出来。Wt递推公式在下面的伪代码有。

step5 ：所有的512-bit分组处理完毕后，对于SHA-256算法最后一个分组产生的输出便是256-bit的报文摘要。

SHA256计算流程

这里面公式太多，就直接截图了。

伪代码实现

可参考https://en.wikipedia.org/wiki/SHA-2。

RIPEMD160

RIPEMD (RACE Integrity Primitives Evaluation Message Digest，RACE原始完整性校验讯息摘要)是一种加密哈希函数。RIPEMD-160是以原始版RIPEMD所改进的160位元版本，而且是RIPEMD系列中最常见的版本。更多请参考：https://homes.esat.kuleuven.be/~bosselae/ripemd160.html

哈希函数在比特币中的应用

在比特币中，应用了两个密码学哈希函数，一个是SHA256，另一个是RIPEMD160，用于比特币地址的生成。下图为比特币地址（账户）的生成流程：

通过随机数发生器生成一个256bit的随机数，并使用该随机数作为账户的私钥。
比特币采用椭圆曲线签名算法（ECDSA）来对数据进行签名和验证，具体使用的是secp256k1曲线。通过ECC乘法可以计算出对应的公钥。
对公钥进行两次散列运算，得到公钥的散列值。
公钥散列值加上版本号和校验码后，进行base58编码可得到地址

Merkle树哈希指针链

哈希指针是一种数据结构，哈希指针指示某些信息存储在何处，我们将这个指针与这些信息的密码学哈希值存储在一起。哈希指针不仅是一种检索信息的方法，同时它也是一种检查信息是否被修改过的方法。

上面的图表示了一个哈希指针，哈希指针是一个指向存储地点的指针，加上一个针对存储时信息的哈希值。

区块链就可以看作一类使用哈希指针的链表。这个链表链接一系列的区块，每个区块包含数据以及指向表中前一个区块的指针。区块链中，前一个区块指针由哈希指针所替换，因此每个区块不仅仅告诉前一个区块的位置，也提供一个哈希值去验证这个区块所包含的数据是否发生改变。

Merkle哈希树

Merkle哈希树是一类基于哈希值的二叉树或多叉树，其叶子节点上的值通常为数据块的哈希值，而非叶子节点上的值，是将该节点的所有子节点的组合结果的哈希值。

Merkle树一般用来进行完整性验证处理。在处理完整性验证的应用场景中，Merkle树会大大减少数据的传输量及计算的复杂度。

成员证明。如果想要证明一个确切的数据块是Merkle树中的一员。通常，只需要树根及这个区块和通向树根沿途的中间哈希值，就可以暂时忽略树的其他部分，这些就已经足以让我们验证到树根。

区块链中的Merkle树是二叉树，如果在树上有<span class="MathJax" id="MathJax-Element-1921-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn个节点，那么就只有<span class="MathJax" id="MathJax-Element-1922-Frame" tabindex="0" data-mathml="log(n)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">log(n)log(n)个块需要被展示。因为每一个步骤都只需要计算下一级块的哈希，所以这大概只需要<span class="MathJax" id="MathJax-Element-1923-Frame" tabindex="0" data-mathml="log(n)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">log(n)log(n)次去证明它。所以即使这个Merkle 树包含了非常多的块，我们依旧可以在一个较短的时间内证明一个成员块。

公钥密码算法公钥密码体制(Public-key cryptography)

公钥密码体制的两个重要原则：

要求在加密算法和公钥都公开的前提下，其加密的密文必须是安全的。
要求所有加密的人和掌握私人密钥的解密人，他们的计算或处理都应比较简单，但对其他不掌握秘密密钥的人，破译应是极其困难的。

公钥密码算法简介

公钥密码算法中的密钥分为公钥和私钥，用户或系统产生一对密钥，将其中的一个公开，就是公钥，另一个自己保留，就是私钥。一般情况下，通信时，发送方利用公钥对信息进行加密，接收方利用私钥对信息进行解密完成通信。当然，也可用私钥加密，公钥解密。因为加密与解密用的是两个不同的密钥，所以这种算法也叫作非对称加密算法。

公钥密码系统的安全性都是基于难题的可计算问题。如：大数分解问题；计算有限域的离散对数问题；平方剩余问题；椭圆曲线的对数问题等。基于这些问题，就有了各种公钥密码体制。后面要讲的椭圆曲线密码算法是其中之一。

椭圆曲线密码算法

椭圆曲线密码算法（Elliptic Curve Cryptography,ECC）是基于椭圆曲线数学的一种公钥密码算法，其安全性依赖于椭圆曲线离散对数问题的困难性。

下面这3篇文章详细讲述了椭圆曲线密码算法的数学原理，不过是英文版的，但是讲述的非常详细，需要掌握的相关数学概念也讲述的很清楚。
http://andrea.corbellini.name/2015/05/17/elliptic-curve-cryptography-a-gentle-introduction/
http://andrea.corbellini.name/2015/05/23/elliptic-curve-cryptography-finite-fields-and-discrete-logarithms/
http://andrea.corbellini.name/2015/05/30/elliptic-curve-cryptography-ecdh-and-ecdsa/
下面这2篇是上面文章的翻译：
http://blog.csdn.net/mrpre/article/details/72850598
http://blog.csdn.net/mrpre/article/details/72850644
这里理论不是很完善，具体的可深入学习Douglas R. Stinson的《密码学原理与实践》。

椭圆曲线密码算法优点

短的密钥长度，意味着小的带宽和存储要求。
所有的用户可以选择同一基域上的不同的椭圆曲线，可使所有的用户使用同样的操作完成域运算。

椭圆曲线定义

设<span class="MathJax" id="MathJax-Element-1946-Frame" tabindex="0" data-mathml="p" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">pp是一个大于3的素数，在有限域<span class="MathJax" id="MathJax-Element-1947-Frame" tabindex="0" data-mathml="Fp" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">FpFp上的椭圆曲线<span class="MathJax" id="MathJax-Element-1948-Frame" tabindex="0" data-mathml="y2=x3+ax+b" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">y2=x3+ax+by2=x3+ax+b由一个基于同余式<span class="MathJax" id="MathJax-Element-1949-Frame" tabindex="0" data-mathml="y2=x3+ax+b mod p" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">y2=x3+ax+b mod py2=x3+ax+b mod p的解集<span class="MathJax" id="MathJax-Element-1950-Frame" tabindex="0" data-mathml="(x,y)∈Fp×Fp" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">(x,y)∈Fp×Fp(x,y)∈Fp×Fp和一个无穷远点的特定点<span class="MathJax" id="MathJax-Element-1951-Frame" tabindex="0" data-mathml="O" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">OO组成，这里<span class="MathJax" id="MathJax-Element-1952-Frame" tabindex="0" data-mathml="a,b∈Fp" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">a,b∈Fpa,b∈Fp是满足<span class="MathJax" id="MathJax-Element-1953-Frame" tabindex="0" data-mathml="4a3+27b2≠0 mod p" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">4a3+27b2≠0 mod p4a3+27b2≠0 mod p的常数。

下图是显示了其中一种实际的椭圆曲线：

对椭圆曲线上的点，我们可以定义一种形式的加法：如果椭圆曲线上的三个点位于同一直线上，那么它们的和为<span class="MathJax" id="MathJax-Element-1954-Frame" tabindex="0" data-mathml="O" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">OO（无穷远点）。

根据上面的定义导出椭圆曲线上的加法运算法则如下：
当<span class="MathJax" id="MathJax-Element-1955-Frame" tabindex="0" data-mathml="P≠Q" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">P≠QP≠Q时：

当<span class="MathJax" id="MathJax-Element-1956-Frame" tabindex="0" data-mathml="P=Q" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">P=QP=Q时：

下面的动画解释了为什么是切线：

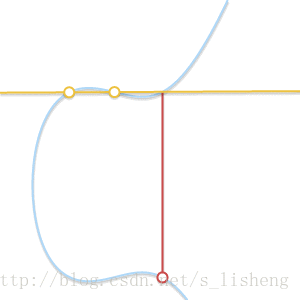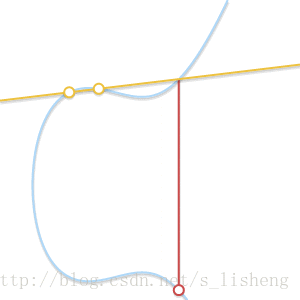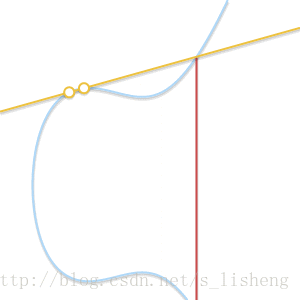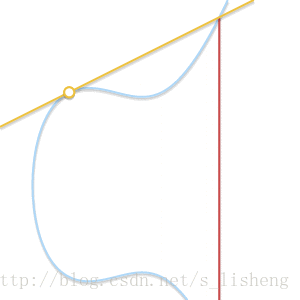
随着两个点越来越接近，过这两点的直线最终变成了曲线的切线

上面用几何的形式解释了椭圆曲线上的加法法则，下面是数学表达式。设<span class="MathJax" id="MathJax-Element-1957-Frame" tabindex="0" data-mathml="P1=(x1,y1)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">P1=(x1,y1)P1=(x1,y1)与<span class="MathJax" id="MathJax-Element-1958-Frame" tabindex="0" data-mathml="P2=(x2,y2)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">P2=(x2,y2)P2=(x2,y2)为椭圆曲线上的两个点，加减法运算如下：
1） <span class="MathJax" id="MathJax-Element-1959-Frame" tabindex="0" data-mathml="−O=O" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">−O=O−O=O
2） <span class="MathJax" id="MathJax-Element-1960-Frame" tabindex="0" data-mathml="−P1=(x1,−y1)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">−P1=(x1,−y1)−P1=(x1,−y1)
3） <span class="MathJax" id="MathJax-Element-1961-Frame" tabindex="0" data-mathml="O+P1=P1" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">O+P1=P1O+P1=P1
4）若<span class="MathJax" id="MathJax-Element-1962-Frame" tabindex="0" data-mathml="P2=−P1" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">P2=−P1P2=−P1，则<span class="MathJax" id="MathJax-Element-1963-Frame" tabindex="0" data-mathml="P1+P2=O" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">P1+P2=OP1+P2=O
5）若<span class="MathJax" id="MathJax-Element-1964-Frame" tabindex="0" data-mathml="P2≠−P1" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">P2≠−P1P2≠−P1，则<span class="MathJax" id="MathJax-Element-1965-Frame" tabindex="0" data-mathml="P1+P2=(x3,y3)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">P1+P2=(x3,y3)P1+P2=(x3,y3)，其中<span class="MathJax" id="MathJax-Element-1966-Frame" tabindex="0" data-mathml="x3=m2−x1−x2" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">x3=m2−x1−x2x3=m2−x1−x2，<span class="MathJax" id="MathJax-Element-1967-Frame" tabindex="0" data-mathml="−y3=m(x3−x1)+y1" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">−y3=m(x3−x1)+y1−y3=m(x3−x1)+y1，

椭圆曲线上点群的离散对数问题

给定椭圆曲线上的点<span class="MathJax" id="MathJax-Element-2183-Frame" tabindex="0" data-mathml="P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">PP和点<span class="MathJax" id="MathJax-Element-2184-Frame" tabindex="0" data-mathml="Q" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">QQ，寻找数<span class="MathJax" id="MathJax-Element-2185-Frame" tabindex="0" data-mathml="k" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">kk，使得<span class="MathJax" id="MathJax-Element-2186-Frame" tabindex="0" data-mathml="kP=Q" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">kP=QkP=Q，其中<span class="MathJax" id="MathJax-Element-2187-Frame" tabindex="0" data-mathml="k" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">kk称为<span class="MathJax" id="MathJax-Element-2188-Frame" tabindex="0" data-mathml="Q" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">QQ的基于<span class="MathJax" id="MathJax-Element-2189-Frame" tabindex="0" data-mathml="P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">PP的离散对数。

在等式<span class="MathJax" id="MathJax-Element-2190-Frame" tabindex="0" data-mathml="kP=P+P+⋯+P=Q" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">kP=P+P+⋯+P=QkP=P+P+⋯+P=Q中，已知<span class="MathJax" id="MathJax-Element-2191-Frame" tabindex="0" data-mathml="k" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">kk和点<span class="MathJax" id="MathJax-Element-2192-Frame" tabindex="0" data-mathml="P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">PP，求点<span class="MathJax" id="MathJax-Element-2193-Frame" tabindex="0" data-mathml="Q" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">QQ比较容易，反之已知点<span class="MathJax" id="MathJax-Element-2194-Frame" tabindex="0" data-mathml="Q" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">QQ和点<span class="MathJax" id="MathJax-Element-2195-Frame" tabindex="0" data-mathml="P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">PP，求<span class="MathJax" id="MathJax-Element-2196-Frame" tabindex="0" data-mathml="k" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">kk却是相当苦难的，这个问题称为椭圆曲线上点群的离散对数问题。椭圆曲线密码体制正是利用这个困难问题设计的。在实际应用中，<span class="MathJax" id="MathJax-Element-2197-Frame" tabindex="0" data-mathml="k" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">kk作为私钥，而<span class="MathJax" id="MathJax-Element-2198-Frame" tabindex="0" data-mathml="Q" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">QQ作为公钥。

如何计算kP=P+P+⋯+P=QkP=P+P+⋯+P=Q

用这种形式表示时，计算<span class="MathJax" id="MathJax-Element-2200-Frame" tabindex="0" data-mathml="kP" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">kPkP似乎需要<span class="MathJax" id="MathJax-Element-2201-Frame" tabindex="0" data-mathml="k" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">kk次加法运算。如果<span class="MathJax" id="MathJax-Element-2202-Frame" tabindex="0" data-mathml="k" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">kk有<span class="MathJax" id="MathJax-Element-2203-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn个二进制位，那么算法的时间复杂度将为<span class="MathJax" id="MathJax-Element-2204-Frame" tabindex="0" data-mathml="O(2n)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">O(2n)O(2n)，这真不是很好。存在一些更快的算法。其中一种是“加倍（double)与相加（add)”算法。计算的原理可以用一个例子来更好地解释。取<span class="MathJax" id="MathJax-Element-2205-Frame" tabindex="0" data-mathml="n=151" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">n=151n=151。它的二进制表示形式为<span class="MathJax" id="MathJax-Element-2206-Frame" tabindex="0" data-mathml="100101112" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">100101112100101112 。这一二进制表示形式可以转换为一系列<span class="MathJax" id="MathJax-Element-2207-Frame" tabindex="0" data-mathml="2" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">22的幂之和。

(取<span class="MathJax" id="MathJax-Element-2208-Frame" tabindex="0" data-mathml="k" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">kk的每个二进制位上的数字，并用它乘以一个<span class="MathJax" id="MathJax-Element-2209-Frame" tabindex="0" data-mathml="2" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">22的幂.)
用这种方法，我们可以将<span class="MathJax" id="MathJax-Element-2210-Frame" tabindex="0" data-mathml="k" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">kk这样写:

“加倍（double)与相加（add)”算法需要这样做:
• 取<span class="MathJax" id="MathJax-Element-2211-Frame" tabindex="0" data-mathml="P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">PP.
• 加倍，得到<span class="MathJax" id="MathJax-Element-2212-Frame" tabindex="0" data-mathml="2P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">2P2P.
• <span class="MathJax" id="MathJax-Element-2213-Frame" tabindex="0" data-mathml="2P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">2P2P与<span class="MathJax" id="MathJax-Element-2214-Frame" tabindex="0" data-mathml="P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">PP相加(为了得到 <span class="MathJax" id="MathJax-Element-2215-Frame" tabindex="0" data-mathml="21P+20P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">21P+20P21P+20P).
• 加倍 <span class="MathJax" id="MathJax-Element-2216-Frame" tabindex="0" data-mathml="2P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">2P2P，得到<span class="MathJax" id="MathJax-Element-2217-Frame" tabindex="0" data-mathml="22P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">22P22P.
• 与前一结果相加 (得到 <span class="MathJax" id="MathJax-Element-2218-Frame" tabindex="0" data-mathml="22P+21P+20P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">22P+21P+20P22P+21P+20P).
• 加倍 <span class="MathJax" id="MathJax-Element-2219-Frame" tabindex="0" data-mathml="22P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">22P22P，得到<span class="MathJax" id="MathJax-Element-2220-Frame" tabindex="0" data-mathml="23P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">23P23P.
• 对<span class="MathJax" id="MathJax-Element-2221-Frame" tabindex="0" data-mathml="23P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">23P23P不做任何操作.
• 加倍<span class="MathJax" id="MathJax-Element-2222-Frame" tabindex="0" data-mathml="23P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">23P23P，得到<span class="MathJax" id="MathJax-Element-2223-Frame" tabindex="0" data-mathml="24P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">24P24P.
• 与前一结果相加 (得到 <span class="MathJax" id="MathJax-Element-2224-Frame" tabindex="0" data-mathml="24P+22P+21P+20P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">24P+22P+21P+20P24P+22P+21P+20P).
• …
最后，我们可以计算<span class="MathJax" id="MathJax-Element-2225-Frame" tabindex="0" data-mathml="151•P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">151∙P151•P，只需7次“加倍”运算和4次“相加”运算。

secp256k1椭圆曲线

比特币系统的区块链实现中使用的椭圆曲线为secp256k1。所以这里需要学习一下。
secp256k1曲线形如<span class="MathJax" id="MathJax-Element-1891-Frame" tabindex="0" data-mathml="y2=x3+ax+b" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">y2=x3+ax+by2=x3+ax+b，由六元组<span class="MathJax" id="MathJax-Element-1892-Frame" tabindex="0" data-mathml="D=(p,a,b,G,n,h)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">D=(p,a,b,G,n,h)D=(p,a,b,G,n,h)定义，其中：
<span class="MathJax" id="MathJax-Element-1893-Frame" tabindex="0" data-mathml="p=FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F=2256−232−29−28−27−26−24−1" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">p=FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F=2256−232−29−28−27−26−24−1p=FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F=2256−232−29−28−27−26−24−1
<span class="MathJax" id="MathJax-Element-1894-Frame" tabindex="0" data-mathml="a=0000000000000000000000000000000000000000000000000000000000000000" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">a=0000000000000000000000000000000000000000000000000000000000000000a=0000000000000000000000000000000000000000000000000000000000000000
<span class="MathJax" id="MathJax-Element-1895-Frame" tabindex="0" data-mathml="b=0000000000000000000000000000000000000000000000000000000000000007" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">b=0000000000000000000000000000000000000000000000000000000000000007b=0000000000000000000000000000000000000000000000000000000000000007
The base point G in compressed form is（压缩形式表示的基点G定义）:
<span class="MathJax" id="MathJax-Element-1896-Frame" tabindex="0" data-mathml="G=0279BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">G=0279BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798G=0279BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
and in uncompressed form is（非压缩形式表示）:
<span class="MathJax" id="MathJax-Element-1897-Frame" tabindex="0" data-mathml="G=0479BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">G=0479BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8G=0479BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8
Finally the order n of G and the cofactor are（G的阶、协因子）:

G的阶：<span class="MathJax" id="MathJax-Element-1898-Frame" tabindex="0" data-mathml="n=FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">n=FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141n=FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
协因子：<span class="MathJax" id="MathJax-Element-1899-Frame" tabindex="0" data-mathml="h=01" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">h=01h=01
secp256k1椭圆曲线形状如下：

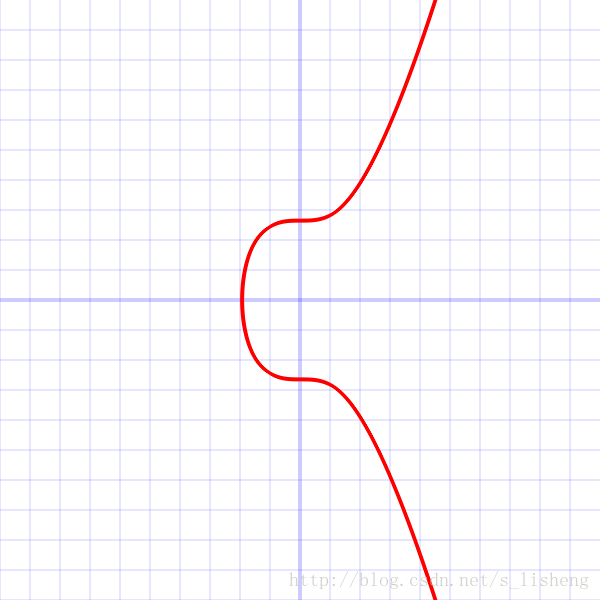
This is a graph of secp256k1’s elliptic curve <span class="MathJax" id="MathJax-Element-1900-Frame" tabindex="0" data-mathml="y2=x3+7" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">y2=x3+7y2=x3+7 over the real numbers. Note that because secp256k1 is actually defined over the field <span class="MathJax" id="MathJax-Element-1901-Frame" tabindex="0" data-mathml="Zp" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">ZpZp, its graph will in reality look like random scattered points, not anything like this.
详细参考：https://en.bitcoin.it/wiki/Secp256k1

椭圆曲线参数六元组解释：
我们的椭圆曲线算法是工作在循环子群上的。几个参数含义如下：
（1）素数<span class="MathJax" id="MathJax-Element-1902-Frame" tabindex="0" data-mathml="p" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">pp，这个值定义了有限域的大小
（2）椭圆曲线的系数<span class="MathJax" id="MathJax-Element-1903-Frame" tabindex="0" data-mathml="a" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">aa、<span class="MathJax" id="MathJax-Element-1904-Frame" tabindex="0" data-mathml="b" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">bb
（3）基点<span class="MathJax" id="MathJax-Element-1905-Frame" tabindex="0" data-mathml="G" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">GG（子群的生成元）
（4）子群的阶<span class="MathJax" id="MathJax-Element-1906-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn
（5）协因子<span class="MathJax" id="MathJax-Element-1907-Frame" tabindex="0" data-mathml="h" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">hh (<span class="MathJax" id="MathJax-Element-1908-Frame" tabindex="0" data-mathml="h=N/n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">h=N/nh=N/n)

ECDSA椭圆曲线数字签名生成

假设Alice希望对消息<span class="MathJax" id="MathJax-Element-130-Frame" tabindex="0" data-mathml="m" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">mm进行签名，她所采用的椭圆曲线参数为<span class="MathJax" id="MathJax-Element-131-Frame" tabindex="0" data-mathml="D=(p,a,b,G,n,h)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">D=(p,a,b,G,n,h)D=(p,a,b,G,n,h)，对应的密钥对为<span class="MathJax" id="MathJax-Element-132-Frame" tabindex="0" data-mathml="(k,Q)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">(k,Q)(k,Q)，其中<span class="MathJax" id="MathJax-Element-133-Frame" tabindex="0" data-mathml="Q" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">QQ为公钥，<span class="MathJax" id="MathJax-Element-134-Frame" tabindex="0" data-mathml="k" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">kk为私钥。Alice将按如下步骤进行签名：
第1步，产生一个随机数<span class="MathJax" id="MathJax-Element-135-Frame" tabindex="0" data-mathml="d" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">dd，<span class="MathJax" id="MathJax-Element-136-Frame" tabindex="0" data-mathml="1≤d≤n−1" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">1≤d≤n−11≤d≤n−1； （为什么是这个范围呢？在下面的”椭圆曲线的数乘和循环子群“及”子群的阶“中有讲述，这是个循环子群）
第2步，计算<span class="MathJax" id="MathJax-Element-137-Frame" tabindex="0" data-mathml="dG=(x1,y1)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">dG=(x1,y1)dG=(x1,y1)，将<span class="MathJax" id="MathJax-Element-138-Frame" tabindex="0" data-mathml="x1" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">x1x1转化为整数<span class="MathJax" id="MathJax-Element-139-Frame" tabindex="0" data-mathml="x1¯" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">x1¯¯¯¯¯x1¯；
第3步，计算<span class="MathJax" id="MathJax-Element-140-Frame" tabindex="0" data-mathml="r=x1¯ mod n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">r=x1¯¯¯¯¯ mod nr=x1¯ mod n，若<span class="MathJax" id="MathJax-Element-141-Frame" tabindex="0" data-mathml="r=0" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">r=0r=0，则转向第1步；
第4步，计算<span class="MathJax" id="MathJax-Element-142-Frame" tabindex="0" data-mathml="d−1 mod n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">d−1 mod nd−1 mod n；
第5步，计算哈希值<span class="MathJax" id="MathJax-Element-143-Frame" tabindex="0" data-mathml="H(m)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">H(m)H(m)，并将得到的比特串转化为整数<span class="MathJax" id="MathJax-Element-144-Frame" tabindex="0" data-mathml="e" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">ee；
第6步，计算<span class="MathJax" id="MathJax-Element-145-Frame" tabindex="0" data-mathml="s=d−1(e+kr) mod n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">s=d−1(e+kr) mod ns=d−1(e+kr) mod n，若<span class="MathJax" id="MathJax-Element-146-Frame" tabindex="0" data-mathml="r=0" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">r=0r=0，则转向第1步；
第7步，<span class="MathJax" id="MathJax-Element-147-Frame" tabindex="0" data-mathml="(r,s)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">(r,s)(r,s)即为Alice对消息<span class="MathJax" id="MathJax-Element-148-Frame" tabindex="0" data-mathml="m" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">mm的签名。

<span class="MathJax" id="MathJax-Element-149-Frame" tabindex="0" data-mathml="d−1" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">d−1d−1 is the multiplicative inverse of <span class="MathJax" id="MathJax-Element-150-Frame" tabindex="0" data-mathml="d" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">dd modulo <span class="MathJax" id="MathJax-Element-151-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn.逆元。

椭圆曲线签名验证

为验证Alice对消息<span class="MathJax" id="MathJax-Element-152-Frame" tabindex="0" data-mathml="m" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">mm的签名<span class="MathJax" id="MathJax-Element-153-Frame" tabindex="0" data-mathml="(r,s)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">(r,s)(r,s)，矿工可以得到Alice所用的椭圆曲线参数以及Alice的公钥<span class="MathJax" id="MathJax-Element-154-Frame" tabindex="0" data-mathml="Q" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">QQ。步骤如下：
第1步，验证<span class="MathJax" id="MathJax-Element-155-Frame" tabindex="0" data-mathml="r" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">rr和<span class="MathJax" id="MathJax-Element-156-Frame" tabindex="0" data-mathml="s" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">ss是区间<span class="MathJax" id="MathJax-Element-157-Frame" tabindex="0" data-mathml="[1,n−1]" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">[1,n−1][1,n−1]上的整数；
第2步，计算<span class="MathJax" id="MathJax-Element-158-Frame" tabindex="0" data-mathml="H(m)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">H(m)H(m)并将其转化为整数<span class="MathJax" id="MathJax-Element-159-Frame" tabindex="0" data-mathml="e" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">ee；
第3步，计算<span class="MathJax" id="MathJax-Element-160-Frame" tabindex="0" data-mathml="w=s−1 mod n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">w=s−1 mod nw=s−1 mod n；
第4步，计算<span class="MathJax" id="MathJax-Element-161-Frame" tabindex="0" data-mathml="u1=ew mod n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">u1=ew mod nu1=ew mod n以及<span class="MathJax" id="MathJax-Element-162-Frame" tabindex="0" data-mathml="u2=rw mod n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">u2=rw mod nu2=rw mod n；
第5步，计算<span class="MathJax" id="MathJax-Element-163-Frame" tabindex="0" data-mathml="X=u1G+u2G" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">X=u1G+u2GX=u1G+u2G；
第6步，若<span class="MathJax" id="MathJax-Element-164-Frame" tabindex="0" data-mathml="X=O" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">X=OX=O，则拒绝签名，否则将<span class="MathJax" id="MathJax-Element-165-Frame" tabindex="0" data-mathml="X" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">XX的<span class="MathJax" id="MathJax-Element-166-Frame" tabindex="0" data-mathml="x" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">xx坐标<span class="MathJax" id="MathJax-Element-167-Frame" tabindex="0" data-mathml="x1" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">x1x1转化为整数<span class="MathJax" id="MathJax-Element-168-Frame" tabindex="0" data-mathml="x1¯" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">x1¯¯¯¯¯x1¯，并计算<span class="MathJax" id="MathJax-Element-169-Frame" tabindex="0" data-mathml="v=x1¯ mod n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">v=x1¯¯¯¯¯ mod nv=x1¯ mod n；
第7步，当且仅当<span class="MathJax" id="MathJax-Element-170-Frame" tabindex="0" data-mathml="v=r" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">v=rv=r时，签名通过验证。

为什么是这样计算，具体证明在这篇文章http://andrea.corbellini.name/2015/05/30/elliptic-curve-cryptography-ecdh-and-ecdsa/的这一节Correctness of the algorithm。以后需要深入的时候再看。

补充数学概念

这里所用到的密码学其数学基础主要是《数论》、《代数》。如果想要弄清其原理，这两部分数学基础是需要研读的。

同余式

数学上，同余（英语：congruence modulo，符号：≡）是数论中的一种等价关系。当两个整数除以同一个正整数，若得相同余数，则二整数同余。同余是抽象代数中的同余关系的原型。

两个整数<span class="MathJax" id="MathJax-Element-171-Frame" tabindex="0" data-mathml="a,b," role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">a,b,a,b,若它们除以正整数<span class="MathJax" id="MathJax-Element-172-Frame" tabindex="0" data-mathml="m" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">mm所得到的余数相等，则称<span class="MathJax" id="MathJax-Element-173-Frame" tabindex="0" data-mathml="a,b" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">a,ba,b对于模<span class="MathJax" id="MathJax-Element-174-Frame" tabindex="0" data-mathml="m" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">mm同余，记作<span class="MathJax" id="MathJax-Element-175-Frame" tabindex="0" data-mathml="a≡b" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">a≡ba≡b <span class="MathJax" id="MathJax-Element-176-Frame" tabindex="0" data-mathml="(mod m)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">(mod m)(mod m)。读作<span class="MathJax" id="MathJax-Element-177-Frame" tabindex="0" data-mathml="a" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">aa与<span class="MathJax" id="MathJax-Element-178-Frame" tabindex="0" data-mathml="b" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">bb关于模<span class="MathJax" id="MathJax-Element-179-Frame" tabindex="0" data-mathml="m" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">mm同余。（例 <span class="MathJax" id="MathJax-Element-180-Frame" tabindex="0" data-mathml="26≡14(mod 12)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">26≡14(mod 12)26≡14(mod 12)）。同余式的其他详细参考：https://zh.wikipedia.org/wiki/%E5%90%8C%E9%A4%98

密码学与有限循环群

现代密码学算法和协议中，消息是作为有限空间中的数字或元素来处理的。加密和解密的各种操作必须在消息之间进行变换，以使变换服从有限消息空间内部的封闭性。然而，数的一般运算诸如加减乘除并不满足有限空间内部的封闭性。所以密码算法通常运行于具有某些保持封闭性的代数结构的空间中，这种代数结构就是有限循环群。在数学中，群是一种代数结构，由一个集合以及一个二元运算组成。群必须满足以下四个条件：封闭性，结合律，存在单位元和存在逆元。

群(Group)的定义：
设<span class="MathJax" id="MathJax-Element-1838-Frame" tabindex="0" data-mathml="G" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">GG是一个非空集合，对于<span class="MathJax" id="MathJax-Element-1839-Frame" tabindex="0" data-mathml="G" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">GG中的任意两个元素<span class="MathJax" id="MathJax-Element-1840-Frame" tabindex="0" data-mathml="a,b" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">a,ba,b，乘法运算满足以下条件，那么<span class="MathJax" id="MathJax-Element-1841-Frame" tabindex="0" data-mathml="G" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">GG称为一个群：
(1). 对于<span class="MathJax" id="MathJax-Element-1842-Frame" tabindex="0" data-mathml="G" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">GG中任意元素<span class="MathJax" id="MathJax-Element-1843-Frame" tabindex="0" data-mathml="a,b,c" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">a,b,ca,b,c，有<span class="MathJax" id="MathJax-Element-1844-Frame" tabindex="0" data-mathml="a(bc)=(ab)c" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">a(bc)=(ab)ca(bc)=(ab)c.
(2). 在<span class="MathJax" id="MathJax-Element-1845-Frame" tabindex="0" data-mathml="G" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">GG中存在一个元素<span class="MathJax" id="MathJax-Element-1846-Frame" tabindex="0" data-mathml="e" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">ee，它对<span class="MathJax" id="MathJax-Element-1847-Frame" tabindex="0" data-mathml="G" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">GG中任意元素<span class="MathJax" id="MathJax-Element-1848-Frame" tabindex="0" data-mathml="a" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">aa有<span class="MathJax" id="MathJax-Element-1849-Frame" tabindex="0" data-mathml="ea=a" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">ea=aea=a.（有单位元）
(3). 对于<span class="MathJax" id="MathJax-Element-1850-Frame" tabindex="0" data-mathml="G" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">GG中任意元素<span class="MathJax" id="MathJax-Element-1851-Frame" tabindex="0" data-mathml="a" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">aa，都存在<span class="MathJax" id="MathJax-Element-1852-Frame" tabindex="0" data-mathml="G" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">GG中一个元素<span class="MathJax" id="MathJax-Element-1853-Frame" tabindex="0" data-mathml="b" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">bb使的<span class="MathJax" id="MathJax-Element-1854-Frame" tabindex="0" data-mathml="ba=e" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">ba=eba=e.（有逆）

最常见的群之一是整数集Z以及加法操作。

有限循环群在群的基础上满足两个额外条件：群元素个数有限以及交换律。循环群由单个元素（产生元）的叠加操作生成，最常见的有限循环群为模拟时钟。

椭圆曲线群定义

在数学上，椭圆曲线群的元素为椭圆曲线上的点，群操作为”+”,”+”的定义为，给定曲线两点<span class="MathJax" id="MathJax-Element-181-Frame" tabindex="0" data-mathml="P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">PP，<span class="MathJax" id="MathJax-Element-182-Frame" tabindex="0" data-mathml="Q" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">QQ，<span class="MathJax" id="MathJax-Element-183-Frame" tabindex="0" data-mathml="P+Q" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">P+QP+Q等于<span class="MathJax" id="MathJax-Element-184-Frame" tabindex="0" data-mathml="P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">PP和<span class="MathJax" id="MathJax-Element-185-Frame" tabindex="0" data-mathml="Q" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">QQ两点的连线与曲线交点沿<span class="MathJax" id="MathJax-Element-186-Frame" tabindex="0" data-mathml="X" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">XX轴的对称点，如果<span class="MathJax" id="MathJax-Element-187-Frame" tabindex="0" data-mathml="P=Q" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">P=QP=Q，则<span class="MathJax" id="MathJax-Element-188-Frame" tabindex="0" data-mathml="P+P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">P+PP+P等于<span class="MathJax" id="MathJax-Element-189-Frame" tabindex="0" data-mathml="P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">PP在曲线上的切线与曲线交点沿<span class="MathJax" id="MathJax-Element-190-Frame" tabindex="0" data-mathml="X" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">XX轴的对称点。该群的单位元为无穷远零点记作<span class="MathJax" id="MathJax-Element-191-Frame" tabindex="0" data-mathml="O=(0,0)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">O=(0,0)O=(0,0)，有<span class="MathJax" id="MathJax-Element-192-Frame" tabindex="0" data-mathml="P+O=P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">P+O=PP+O=P，点<span class="MathJax" id="MathJax-Element-193-Frame" tabindex="0" data-mathml="P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">PP的逆元为其沿<span class="MathJax" id="MathJax-Element-194-Frame" tabindex="0" data-mathml="X" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">XX轴的对称点，记作<span class="MathJax" id="MathJax-Element-195-Frame" tabindex="0" data-mathml="−P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">−P−P。

椭圆曲线有限循环群

前面介绍的椭圆曲线都是基于有理数的，但是计算机运算浮点数(小数)的速度较慢，更重要的是四舍五入浮点数会产生误差，导致多次加密解密操作后原始消息不能被还原。故考虑到加密算法的可实现性，密码学上使用基于整数的模加运算产生椭圆曲线有限循环群。
基于整数的模加运算的特点：

运算速度快
精确的运算结果
产生有限循环

下面举例说明，如何产生ECC有限循环群：
例如考虑<span class="MathJax" id="MathJax-Element-196-Frame" tabindex="0" data-mathml="y2=x3−7x+10(mod 19)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">y2=x3−7x+10(mod 19)y2=x3−7x+10(mod 19)的集合，该集合中所有的元素如下图所示。模运算把发散的椭圆曲线映射到19*19的正方形空间中，并且保持了原有曲线的上下对称特性。

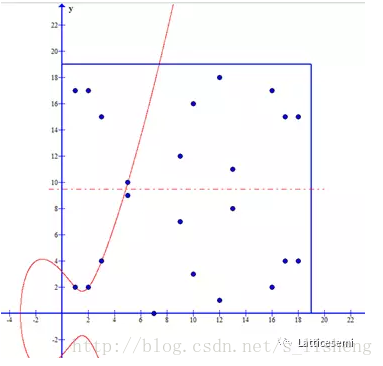
下图展示了<span class="MathJax" id="MathJax-Element-197-Frame" tabindex="0" data-mathml="y2=x3−7x+10(mod 19)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">y2=x3−7x+10(mod 19)y2=x3−7x+10(mod 19)集合中的元素和椭圆曲线的关系。
点<span class="MathJax" id="MathJax-Element-198-Frame" tabindex="0" data-mathml="Q′" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">Q′Q′映射到点<span class="MathJax" id="MathJax-Element-199-Frame" tabindex="0" data-mathml="Q" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">QQ，点<span class="MathJax" id="MathJax-Element-200-Frame" tabindex="0" data-mathml="P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">PP的对称点也由点<span class="MathJax" id="MathJax-Element-201-Frame" tabindex="0" data-mathml="−P′" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">−P′−P′映射到点<span class="MathJax" id="MathJax-Element-202-Frame" tabindex="0" data-mathml="−P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">−P−P。

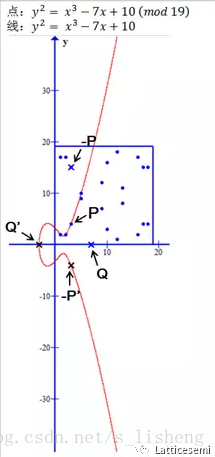
如果取一个更大的质数<span class="MathJax" id="MathJax-Element-203-Frame" tabindex="0" data-mathml="p" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">pp进行模运算，集合中的元素点也会相应地增多。下图展示了利用同一个曲线方程进行不同模运算的结果。在实际的椭圆曲线加密算法中，使用长度为192-256位的质数<span class="MathJax" id="MathJax-Element-204-Frame" tabindex="0" data-mathml="p" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">pp进行模运算。

现在我们基于<span class="MathJax" id="MathJax-Element-205-Frame" tabindex="0" data-mathml="y2=x3−7x+10(mod 19)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">y2=x3−7x+10(mod 19)y2=x3−7x+10(mod 19)，利用产生元<span class="MathJax" id="MathJax-Element-206-Frame" tabindex="0" data-mathml="P=(2,2)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">P=(2,2)P=(2,2)来生成ECC有限循环群。如下图所示。

<span class="MathJax" id="MathJax-Element-207-Frame" tabindex="0" data-mathml="G={nP|P=(2,2)}" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">G={nP|P=(2,2)}G={nP|P=(2,2)}完整的集合为<span class="MathJax" id="MathJax-Element-208-Frame" tabindex="0" data-mathml="{p=(2,2),2P=(13,8),3P=(1,2),4P=(16,17),5P=(10,3),6P=(18,15),7P=(3,15),8P=(12,1),9P=(9,12),10P=(5,10),11P=(17,15),12P=(7,0),13P=(17,4),14P=(5,9),15P=(9,7),16P=(12,18),17P=(3,4),18P=(18,4),19P=(10,16),20P=(16,2),21P=(1,17),22P=(13,11),23P=(2,17),24P=O=(0,0)}" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">{p=(2,2),2P=(13,8),3P=(1,2),4P=(16,17),5P=(10,3),6P=(18,15),7P=(3,15),8P=(12,1),9P=(9,12),10P=(5,10),11P=(17,15),12P=(7,0),13P=(17,4),14P=(5,9),15P=(9,7),16P=(12,18),17P=(3,4),18P=(18,4),19P=(10,16),20P=(16,2),21P=(1,17),22P=(13,11),23P=(2,17),24P=O=(0,0)}{p=(2,2),2P=(13,8),3P=(1,2),4P=(16,17),5P=(10,3),6P=(18,15),7P=(3,15),8P=(12,1),9P=(9,12),10P=(5,10),11P=(17,15),12P=(7,0),13P=(17,4),14P=(5,9),15P=(9,7),16P=(12,18),17P=(3,4),18P=(18,4),19P=(10,16),20P=(16,2),21P=(1,17),22P=(13,11),23P=(2,17),24P=O=(0,0)}。如下图所示，随着<span class="MathJax" id="MathJax-Element-209-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn的连续增加，元素点的分布没有任何特征，这正是密码学需要的特性。

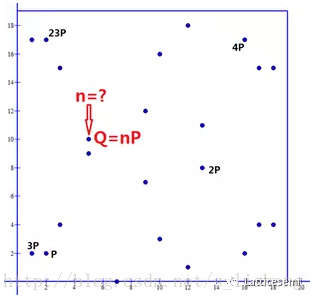
可参考：http://mp.weixin.qq.com/s/jOcVk7olBDgBgoy56m5cxQ

椭圆曲线的阶

椭圆曲线定义在有限域上，这也意味着，椭圆曲线上的点也是有限的。所以引出了一个问题：一个椭圆曲线到底有多少个点？定义“椭圆曲线上点的个数”为椭圆曲线的阶 (order)。至于怎么计算阶参考这篇文章吧： https://en.wikipedia.org/wiki/Schoof%27s_algorithm

椭圆曲线的数乘和循环子群

在实数域，数乘（标量乘法）被定义如下：

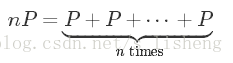
如何计算及算法复杂度，上面有讲过，这里讲述它的一个性质。举例说明：
椭圆曲线<span class="MathJax" id="MathJax-Element-210-Frame" tabindex="0" data-mathml="y2≡x3+2x+3 (mod 97)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">y2≡x3+2x+3 (mod 97)y2≡x3+2x+3 (mod 97)，点<span class="MathJax" id="MathJax-Element-211-Frame" tabindex="0" data-mathml="P=(3,6)" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">P=(3,6)P=(3,6)。现在计算<span class="MathJax" id="MathJax-Element-212-Frame" tabindex="0" data-mathml="P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">PP的数乘。

上图可以化为下图的表示形式：

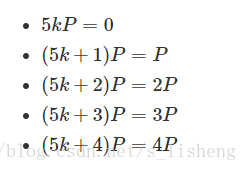
结果显示点<span class="MathJax" id="MathJax-Element-213-Frame" tabindex="0" data-mathml="P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">PP的倍数的结果只有出现5个点，其他的点从未出现；其次他们是周期出现的。显然，上面的5个点的集合，运算是封闭的。
当然，不仅仅<span class="MathJax" id="MathJax-Element-214-Frame" tabindex="0" data-mathml="P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">PP有这样的性质，其他点也有类似的性质。
即，<span class="MathJax" id="MathJax-Element-215-Frame" tabindex="0" data-mathml="P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">PP的加法构成了一个群<span class="MathJax" id="MathJax-Element-216-Frame" tabindex="0" data-mathml="S" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">SS，由于<span class="MathJax" id="MathJax-Element-217-Frame" tabindex="0" data-mathml="S" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">SS属于<span class="MathJax" id="MathJax-Element-218-Frame" tabindex="0" data-mathml="G" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">GG，故<span class="MathJax" id="MathJax-Element-219-Frame" tabindex="0" data-mathml="S" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">SS是<span class="MathJax" id="MathJax-Element-220-Frame" tabindex="0" data-mathml="G" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">GG的子群。
循环子群是ECC的基础。

子群的阶

首先，我们已经定义了阶就是群中点的个数。在子群中也是这样的，但是我们可以换一种表达方式：子群的阶是最小能够使得nP=0nP=0的nn。
子群的阶和群的阶是有关系的。拉格朗日定理说明了，子群的阶是群的阶的因子。即如果NN是群的阶，则其子群的阶nn，则nn是NN的因子（nn is a diviser of NN）。

找到子群的阶的方法（根据上面讲述的定义和性质就能得出下面的方法）：
（1）计算群的阶<span class="MathJax" id="MathJax-Element-229-Frame" tabindex="0" data-mathml="N" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">NN
（2）找出所有<span class="MathJax" id="MathJax-Element-230-Frame" tabindex="0" data-mathml="N" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">NN的因子
（3）每个<span class="MathJax" id="MathJax-Element-231-Frame" tabindex="0" data-mathml="N" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">NN的因子<span class="MathJax" id="MathJax-Element-232-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn，然后乘以<span class="MathJax" id="MathJax-Element-233-Frame" tabindex="0" data-mathml="P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">PP
（4）在3中，找出最小的<span class="MathJax" id="MathJax-Element-234-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn，使得满足<span class="MathJax" id="MathJax-Element-235-Frame" tabindex="0" data-mathml="nP=0" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nP=0nP=0。则<span class="MathJax" id="MathJax-Element-236-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn是子群的阶。

如何找一个基点

在ECC算法种，我们希望找到一个阶数较大的子群。
通常我们会选择一个椭圆曲线，然后计算它的阶<span class="MathJax" id="MathJax-Element-237-Frame" tabindex="0" data-mathml="N" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">NN，选择一个较大的因子<span class="MathJax" id="MathJax-Element-238-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn，然后找一个合适的基点。也就是说，我们不是首先找一个基点，然后计算它的阶，而是相反，我们先找到一个合适的阶，然后找以这个数为阶的子群的生成元。

首先，拉格朗日揭示，<span class="MathJax" id="MathJax-Element-239-Frame" tabindex="0" data-mathml="h=N/n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">h=N/nh=N/n是一个整数（当然，<span class="MathJax" id="MathJax-Element-240-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn是<span class="MathJax" id="MathJax-Element-241-Frame" tabindex="0" data-mathml="N" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">NN的因子），<span class="MathJax" id="MathJax-Element-242-Frame" tabindex="0" data-mathml="h" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">hh有一个自己的名字：cofactor of the subgroup（协因子）。

其次，每个椭圆曲线上的点<span class="MathJax" id="MathJax-Element-243-Frame" tabindex="0" data-mathml="P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">PP，<span class="MathJax" id="MathJax-Element-244-Frame" tabindex="0" data-mathml="NP=0" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">NP=0NP=0，因为<span class="MathJax" id="MathJax-Element-245-Frame" tabindex="0" data-mathml="N" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">NN是<span class="MathJax" id="MathJax-Element-246-Frame" tabindex="0" data-mathml="P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">PP的阶<span class="MathJax" id="MathJax-Element-247-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn的倍数。
我们可以写成这样 <span class="MathJax" id="MathJax-Element-248-Frame" tabindex="0" data-mathml="n(hP)=0" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">n(hP)=0n(hP)=0。
假设<span class="MathJax" id="MathJax-Element-249-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn是一个素数，我们令<span class="MathJax" id="MathJax-Element-250-Frame" tabindex="0" data-mathml="G=hP" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">G=hPG=hP，则<span class="MathJax" id="MathJax-Element-251-Frame" tabindex="0" data-mathml="G" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">GG就是子群的生成元。
<span class="MathJax" id="MathJax-Element-252-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn必须是素数，若非如此，则<span class="MathJax" id="MathJax-Element-253-Frame" tabindex="0" data-mathml="nP=0" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nP=0nP=0不一定表示<span class="MathJax" id="MathJax-Element-254-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn是<span class="MathJax" id="MathJax-Element-255-Frame" tabindex="0" data-mathml="P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">PP的阶，因为<span class="MathJax" id="MathJax-Element-256-Frame" tabindex="0" data-mathml="P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">PP的阶可能是<span class="MathJax" id="MathJax-Element-257-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn的一个因子。
总结如下：
1. 计算椭圆曲线的阶<span class="MathJax" id="MathJax-Element-258-Frame" tabindex="0" data-mathml="N" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">NN。
2. 选择一个数<span class="MathJax" id="MathJax-Element-259-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn当成子群的阶。<span class="MathJax" id="MathJax-Element-260-Frame" tabindex="0" data-mathml="n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">nn应该是<span class="MathJax" id="MathJax-Element-261-Frame" tabindex="0" data-mathml="N" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">NN的素因数
3. 计算<span class="MathJax" id="MathJax-Element-262-Frame" tabindex="0" data-mathml="h=N/n" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">h=N/nh=N/n
4. 随机选择一个点<span class="MathJax" id="MathJax-Element-263-Frame" tabindex="0" data-mathml="P" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">PP
5. 计算<span class="MathJax" id="MathJax-Element-264-Frame" tabindex="0" data-mathml="G=hP" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">G=hPG=hP
6. 如果<span class="MathJax" id="MathJax-Element-265-Frame" tabindex="0" data-mathml="G" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">GG是<span class="MathJax" id="MathJax-Element-266-Frame" tabindex="0" data-mathml="0" role="presentation" style="box-sizing: border-box; outline: 0px; display: inline; line-height: normal; text-align: left; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; word-break: break-all; position: relative;">00，到第4步。否则，我们找到了这个基点。

作者: 不二晨 时间: 2018-9-6 11:42
奈斯

欢迎光临黑马程序员技术交流社区 (http://bbs.itheima.com/)

黑马程序员IT技术论坛 X3.2