黑马程序员技术交流社区
标题: 【文章】java排序算法 [打印本页]
作者: 小蜀哥哥 时间: 2019-12-20 16:07
标题: 【文章】java排序算法
认识时间复杂度
常数时间的操作:一个操作如果和数据量没有关系,每次都是 固定时间内完成的操作,叫做常数操作。
时间复杂度为一个算法流程中,在最差的数据情况下,常数操作数量的指标。常用O (读作big O)来表示。具体来说,在常数操作数量的表达式中, 只要高阶项,不要低阶项,也不要高阶项的系数,剩下的部分 如果记为f(N),那么时间复杂度为O(f(N))。
评价一个算法流程的好坏,先看时间复杂度的指标,然后再分 析不同数据样本下的实际运行时间,也就是常数项时间。
冒泡排序细节的讲解与复杂度分析
时间复杂度O(N^2),额外空间复杂度O(1)
代码实现:
[Java] 纯文本查看 复制代码
public static void bubbleSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int e = arr.length - 1; e > 0; e--) {
for (int i = 0; i < e; i++) {
if (arr > arr[i + 1]) {
swap(arr, i, i + 1);
}
}
}
}
public static void swap(int[] arr, int i, int j) {
arr = arr ^ arr[j];
arr[j] = arr ^ arr[j];
arr = arr ^ arr[j];
}
选择排序的细节讲解与复杂度分析
时间复杂度O(N^2),额外空间复杂度O(1)
代码实现:
[Java] 纯文本查看 复制代码
public static void selectionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) {
minIndex = arr[j] < arr[minIndex] ? j : minIndex;
}
swap(arr, i, minIndex);
}
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr;
arr = arr[j];
arr[j] = tmp;
}
插入排序的细节讲解与复杂度分析
时间复杂度O(N^2),额外空间复杂度O(1)
代码实现:
[Java] 纯文本查看 复制代码
public static void insertionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 1; i < arr.length; i++) {
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
swap(arr, j, j + 1);
}
}
}
public static void swap(int[] arr, int i, int j) {
arr = arr ^ arr[j];
arr[j] = arr ^ arr[j];
arr = arr ^ arr[j];
}
对数器的概念和使用
有一个你想要测的方法a;
实现一个绝对正确但是复杂度不好的方法b;
实现一个随机样本产生器 ;
实现比对的方法 ;
把方法a和方法b比对很多次来验证方法a是否正确;
如果有一个样本使得比对出错,打印样本分析是哪个方法出错 ;
当样本数量很多时比对测试依然正确,可以确定方法a已经 正确。
我们以冒泡排序为例
代码如下:
[Java] 纯文本查看 复制代码
import java.util.Arrays;
public class BubbleSort {
public static void bubbleSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int e = arr.length - 1; e > 0; e--) {
for (int i = 0; i < e; i++) {
if (arr > arr[i + 1]) {
swap(arr, i, i + 1);
}
}
}
}
public static void swap(int[] arr, int i, int j) {
arr = arr ^ arr[j];
arr[j] = arr ^ arr[j];
arr = arr ^ arr[j];
}
// for test
public static void comparator(int[] arr) {
Arrays.sort(arr);
}
// for test
public static int[] generateRandomArray(int maxSize, int maxValue) {
int[] arr = new int[(int) ((maxSize + 1) * Math.random())];
for (int i = 0; i < arr.length; i++) {
arr = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());
}
return arr;
}
// for test
public static int[] copyArray(int[] arr) {
if (arr == null) {
return null;
}
int[] res = new int[arr.length];
for (int i = 0; i < arr.length; i++) {
res = arr;
}
return res;
}
// for test
public static boolean isEqual(int[] arr1, int[] arr2) {
if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {
return false;
}
if (arr1 == null && arr2 == null) {
return true;
}
if (arr1.length != arr2.length) {
return false;
}
for (int i = 0; i < arr1.length; i++) {
if (arr1 != arr2) {
return false;
}
}
return true;
}
// for test
public static void printArray(int[] arr) {
if (arr == null) {
return;
}
for (int i = 0; i < arr.length; i++) {
System.out.print(arr + " ");
}
System.out.println();
}
// for test
public static void main(String[] args) {
int testTime = 500000;
int maxSize = 100;
int maxValue = 100;
boolean succeed = true;
for (int i = 0; i < testTime; i++) {
int[] arr1 = generateRandomArray(maxSize, maxValue);
int[] arr2 = copyArray(arr1);
bubbleSort(arr1);
comparator(arr2);
if (!isEqual(arr1, arr2)) {
succeed = false;
break;
}
}
System.out.println(succeed ? "Nice!" : "Fucking fucked!");
int[] arr = generateRandomArray(maxSize, maxValue);
printArray(arr);
bubbleSort(arr);
printArray(arr);
}
}
平时设计或者阅读一个算法的时候,必然会提到算法的复杂度(包括时间复杂度和空间复杂度)。比如我们说一个二分查找算法的平均时间复杂度为O(log n),快速排序可能是O(n log n)。那这里的O是什么意思?这样的表达是否准确呢?
今天来复习一下与算法复杂度相关的知识:函数渐进阶,记号O、Ω、θ和o;Master定理。
先插一句,在算法复杂度分析中,log通常表示以2为底的对数。
算法复杂度(算法复杂性)是用来衡量算法运行所需要的计算机资源(时间、空间)的量。通常我们利用渐进性态来描述算法的复杂度。
用n表示问题的规模,T(n)表示某个给定算法的复杂度。所谓渐进性态就是令n→∞时,T(n)中增长最快的那部分。严格的定义是:如果存在T˜(n)T~(n),当n→∞时,有

比如T(n) = 2 * n ^ 2 + n log n + 3,那么显然它的渐进性态是 2 * n ^ 2,因为当n→∞时,后两项的增长速度要慢的多,可以忽略掉。引入渐进性态是为了简化算法复杂度的表达式,只考虑其中的主要因素。当比较两个算法复杂度的时候,如果他们的渐进复杂度的阶不相同,那只需要比较彼此的阶(忽略常数系数)就可以了。
总之,分析算法复杂度的时候,并不用严格演算出一个具体的公式,而是只需要分析当问题规模充分大的时候,复杂度在渐进意义下的阶。记号O、Ω、θ和o可以帮助我们了解函数渐进阶的大小。

假设有两个函数f(n)和g(n),都是定义在正整数集上的正函数。上述四个记号的含义分别是:
可见,记号O给出了函数f(n)在渐进意义下的上界(但不一定是最小的),相反,记号Ω给出的是下界(不一定是最大的)。如果上界与下界相同,表示f(n)和g(n)在渐进意义下是同阶的(θ),亦即复杂度一样。
列举一些常见的函数之间的渐进阶的关系:
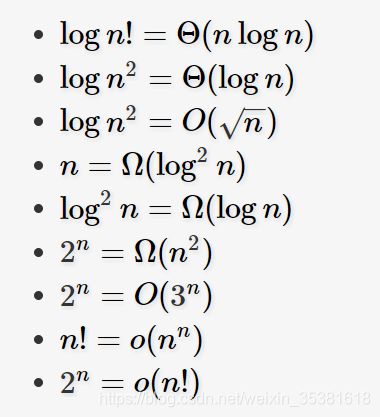
有些人可能会把这几个记号跟算法的最坏、最好、平均情况复杂度混淆,它们有区别,也有一定的联系。
即使问题的规模相同,随着输入数据本身属性的不同,算法的处理时间也可能会不同。于是就有了最坏情况、最好情况和平均情况下算法复杂度的区别。它们从不同的角度反映了算法的效率,各有用处,也各有局限。
有时候也可以利用最坏情况、最好情况下算法复杂度来粗略地估计算法的性能。比如某个算法在最坏情况下时间复杂度为θ(n ^ 2),最好情况下为θ(n),那这个算法的复杂度一定是O(n ^ 2)、Ω(n)的。也就是说n ^ 2是该算法复杂度的上界,n是其下界。
接下来看看Master定理。
有些算法在处理一个较大规模的问题时,往往会把问题拆分成几个子问题,对其中的一个或多个问题递归地处理,并在分治之前或之后进行一些预处理、汇总处理。这时候我们可以得到关于这个算法复杂度的一个递推方程,求解此方程便能得到算法的复杂度。其中很常见的一种递推方程就是这样的:
设常数a >= 1,b > 1,f(n)为函数,T(n)为非负整数,T(n) = a T(n / b) + f(n),则有:
比如常见的二分查找算法,时间复杂度的递推方程为T(n) = T(n / 2) + θ(1),显然有nlogba=n0=Θ(1)nlogba=n0=Θ(1),满足Master定理第二条,可以得到其时间复杂度为T(n) = θ(log n)。
再看一个例子,T(n) = 9 T(n / 3) + n,可知nlogba=n2nlogba=n2,令ε取1,显然满足Master定理第一条,可以得到T(n) = θ(n ^ 2)。
来一个稍微复杂一点儿例子,T(n) = 3 T(n / 4) + n log n。nlogba=O(n0.793)nlogba=O(n0.793),取ε = 0.2,显然当c = 3 / 4时,对于充分大的n可以满足a * f(n / b) = 3 * (n / 4) * log(n / 4) <= (3 / 4) * n * log n = c * f(n),符合Master定理第三条,因此求得T(n) = θ(n log n)。

运用Master定理的时候,有一点一定要特别注意,就是第一条和第三条中的ε必须大于零。如果无法找到大于零的ε,就不能使用这两条规则。
举个例子,T(n) = 2 T(n / 2) + n log n。可知nlogba=n1nlogba=n1,而f(n) = n log n,显然不满足Master定理第二条。但对于第一条和第三条,也无法找到大于零的ε使得nlogn=O(n1−ε)nlogn=O(n1−ε)或者nlogn=Ω(n1+ε)nlogn=Ω(n1+ε),因此不能用Master定理求解,只能寻求别的方式求解。比如可以利用递归树求出该算法的复杂度为T(n)=O(nlog2n)T(n)=O(nlog2n)。简单的说一下计算过程:
递归树的建立过程,就像是模拟算法的递推过程。树根对应的是输入的规模为n的问题,在递归处理子问题之外,还需要n log n的处理时间。然后根据递推公式给根节点添加子节点,每个子节点对应一个子问题。这里需要两个子节点,每个节点处理规模为n / 2的问题,分别需要(n / 2) * log(n / 2)的时间。因此在第二层一共需要n * (log n - 1)的时间。第三层节点就是将第二层的两个节点继续分裂开,得到四个各需要(n / 4) * log(n / 4)时间的节点,总的时间消耗为n * (log n - 2)。依此类推,第k(设树根为k = 0)层有2 ^ k的节点,总的时间为n * (log n - k)。而且可以知道,这棵树总共有log n层(最后一层每个节点只处理规模为1的子问题,无须再分治)。最后将每一层消耗的时间累加起来,得到:
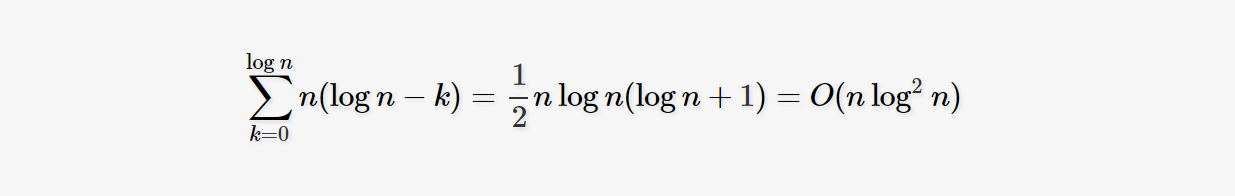
| 欢迎光临 黑马程序员技术交流社区 (http://bbs.itheima.com/) |
黑马程序员IT技术论坛 X3.2 |